Michael Essien
What would be the perfect, all-encompassing football statistic? Something that takes in to account both offensive and defensive skill. Something that measures what value a player adds to his club. All in all, a statistic that quantifies the individual impact a player has on improving (or worsening) his club's ability to score goals and limit (or not) goals against.
Some people have made attempts at this in the past. One example are OptaJoe's tweets (@OptaJoe) about club's winning percentages with and without a player. Here is one example: "10 - Since January 2005, Everton have averaged 61 points per season with Arteta playing, compared to 51 points without him. Lynchpin." These statements are simple, easy to understand, and at first glance seem to be informative. On his blog 5 Added Minutes, Omar Chaudhuri has correctly pointed out that these statements tend to be entirely misleading. As Omar shows, the problem is that these statements are not controlling for the strength of the opponent, the venue of the game, or really anything else, in these games.
My idea was to create a metric that would control for all of these factors to truly understand every player's worth to their club. Being a big ice hockey fan (specifically the Boston Bruins, if you are wondering) I thought that the plus minus statistic might be able to be applied to football. For those of you not familiar with this statistic, plus minus basically measures a club's net goals when that player is on the ice/field. When the team scores a goal when the player is playing, the player's plus minus increases by one. Conversely, when their team concedes a goal when they are playing, their plus minus decreases by one. The idea is that, over the season, the best players will have the highest plus minus.
I faced the same problem as before though, as this does not control for the strength of the opponent, the strength of the team the player is playing with, and where the game is being played. For example, a poor player on a top club would naturally have a higher plus minus than a good player on a poor club.
To fix this, I applied an analysis used in basketball to create an adjusted plus minus statistic. This was created by Dan Rosenbaum, and if you are interested the explanation can be found here
Without going in to too many technical details, the adjusted plus minus metric is created using a massive regression. The right hand side variables are variables for every player, while the left hand side are goals for. Each observation is a unit of time during a game where no substitutions are made. Each player variable is a 1 if the player is playing at home during that unit of time, a -1 if they are playing away, and a 0 if they are not playing. The significance behind this methodology is that it controls for each player's team, venue, and opponents. If you want to know more about the methodology, read the link above. The data is from the 2010/2011 season and is provided by Infostrada Sports (@InfostradaLive on Twitter).
The main problem with this as some, including Albert Larcada (@adlarcada_ESPN), pointed out on Twitter, is that there is multicollinearity in the regression. This arises because, unlike in basketball, there are not many scoring events. What happens is that many players are highly correlated in the model. This throws off the adjusted plus minus values for each player, so we should not take anything from the results.
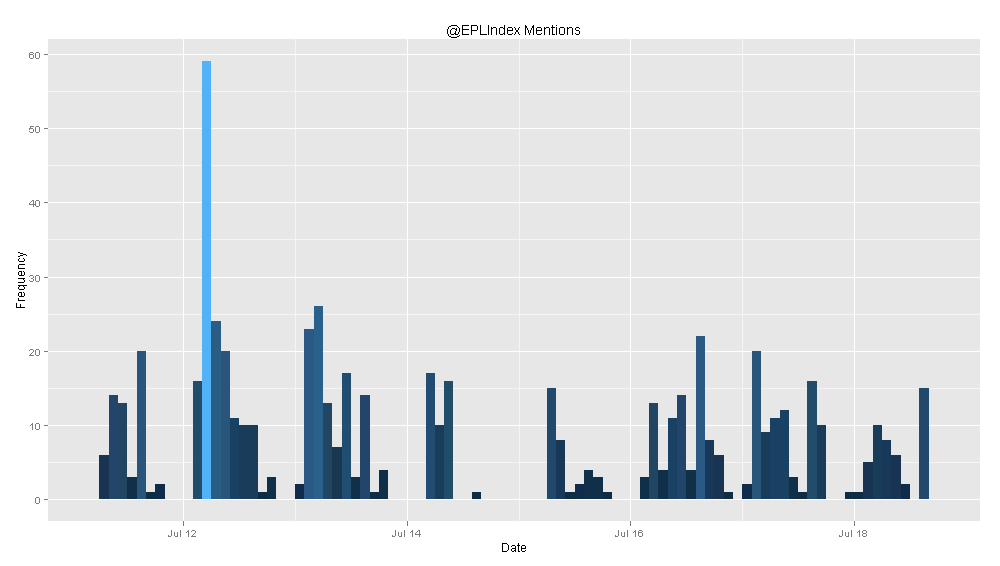
With that in mind, here are the results that I came up with. Again, these results are likely not correct, but I thought people might be curious to see them anyways: